Regression and ANOVA - Sample Size Calculator

Calculates the sample size for the linear regression or for the ANOVA test.

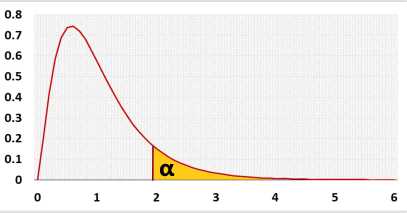
Significance level (α): Predictors (p): Effect type: Effect Size: How to do with R? Power analysis

How to use the calculator?

  1. Type:
    Regression - for linear regression.
    ANOVA - for one sample ANOVA.
  2. Significance level (α): a p-value less than the significance level is statistically significant.
    Researchers usually use 0.05, but if the price of a mistake is big, they may use a smaller value like 0.01.
  3. Power - the test power you want to achieve when using the sample data.
  4. Predictors - the number of independent variables (Xi) in the linear regression.
  5. Groups - the number of groups in the one way ANOVA test.
  6. Effect - If you don't know the required effect size, you may use the 'effect' field. The default is 'Medium', if you change the value, it will change 'effect type' to 'f' and fill the proper value per Cohen's suggestion in the 'effect size' field.
    Regression - (0.14: Small, 0.39: medium, 0.59: large).
    ANOVA - (0.1: Small, 0.25: medium, 0.4: large).
    The calculator will not use this field when pressing the 'calculate' button
  7. Effect type - f or f 2 or R 2 / η 2
  8. Effect size - the value that you want the test to be able to identify. You need a larger sample size to be able to identify a smaller effect size.
  9. Rounding - how to round the results?
    When a resulting value is larger than one, the tool rounds it, but when a resulting value is less than one the tool displays the significant figures.

Regression sample size calculator

  1. Entire model test power - the sample size that achieve the required test power for the entire linear regression model.
    tests if the linear model supports significantly better result than the average.
  2. Green's rule of thumb (medium effect) to test the entire model: n = 50 + 8*predictors
  3. Green's rule of thumb (medium effect) to test the coefficients: n = 104 + predictors

ANOVA sample size calculator

Calculates the sample size for the one way ANOVA test, based on the number of groups and draw a power analysis chart.

Use the calculator for: One way ANOVA

Effect sizes

You may use one of the following effect sizes: Cohen's f, f 2 , R 2 for linear regression, or Cohen's f, f 2 , η 2 for ANOVA.

Regression example:
Linear regression with 4 predictors, α=0.05, power=0.8.
A sample of 85 will identify model with R 2 =0.13. (or f=0.3873 or f 2 =0.15)
i.e. the power of a model with a smaller R 2 will be lower than 0.8 .

ANOVA example:
ANOVA with 3 groups, α=0.05, power=0.8, Medium effect size.
A sample of 158 will identify an effect size of 0.25, with the power of 0.8022.

Distribution

distribution right tailed

R Code

The following R code should produce the same results